我們花了幾天的時間來介紹在如何將單詞轉化為詞向量，用於模型訓練或其他任務，今天就來聊聊如何利用這些詞向量來判斷單詞之間的語意相似度吧。

經過 embedding 之後的單詞在高維空間中可以用一組向量來表示，那麼，要如何衡量他們在語意上是否相似？

我們在國高中的時候有學過歐式距離 ( Euclidean Distance )，它的計算方式是這樣：

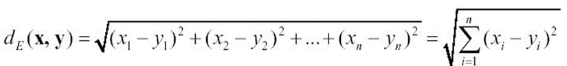
我們的確可以算出兩個向量之間的距離，用來判斷這兩個單詞語意是否一樣，然而對於詞向量而言，單純考慮距離並不能準確反映語意上的相似性，因為詞向量的語意相似性主要取決於它們的方向，而不僅僅是距離的遠近。

Cosine Similarity

因此，我們更常採用的計算方式是餘弦相似度 ( Cosine Similarity )，它可以計算兩個向量之間夾角的餘弦值，當夾角越小，餘弦值越大，也代表兩個單詞之間的相似度越高。

Cosine Similarity 的計算方式是這樣：

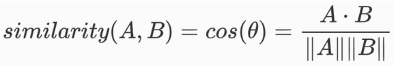
觀察公式可以發現，分子部分使用了點積 ( dot product ) 計算兩個向量的方向是否一致，而分母部分則計算了向量的長度，目的在於消除向量大小造成的影響。

接下來就進入實作部分吧！

首先我們要建立一個 Word2Vec 模型，在這裡要特別提一下，如果資料太少的話訓練出來的模型效果也不好，因此我找了 NLTK 提供的 Brown 語料庫，而訓練的部分則找了 Gensim 的 Word2Vec 工具。

import nltk
from gensim.models import Word2Vec
from nltk.corpus import brown

nltk.download('brown')
sentences = brown.sents()
model = Word2Vec(sentences, vector_size = 100, window = 5, min_count = 1, workers = 4)
model.save("word2vec.model")

訓練後可以先儲存起來，需要的時候再重新載入就好。我們來看一下經過訓練之後，單詞向量化的結果長什麼樣子：

model = Word2Vec.load("word2vec.model")
print(model.wv['good'])

[ 4.77009639e-02  8.14621598e-02  2.19687521e-01  1.17895812e-01
 -1.16647884e-01 -3.35068226e-01  2.49497369e-01  7.13665366e-01
 -3.32638830e-01 -3.29513878e-01 -8.08985904e-03 -4.21775192e-01
  1.20260954e-01 -1.06325440e-01  2.48778626e-01 -1.84106246e-01 ...]

因為我們在訓練模型的時候參數 vector_size 設為 100，所以詞向量的維度就是 100，接下來讓我們看看如何實作餘弦相似度吧。

from sklearn.metrics.pairwise import cosine_similarity
import numpy as np
import pandas as pd

model = Word2Vec.load("word2vec.model")
words = ["he", "we", "kind", "evil"]
vectors = np.array([model.wv[word] for word in words])

similarity_matrix = cosine_similarity(vectors)
similarity_df = pd.DataFrame(similarity_matrix, index = words, columns = words)

print(similarity_df.round(2))

         he    we  kind  evil
he     1.00  0.60  0.38  0.43
we     0.60  1.00  0.53  0.49
kind   0.38  0.53  1.00  0.83
evil   0.43  0.49  0.83  1.00

從輸出結果可以看出，he 和 we 在向量空間中的分布一致，因為他們都是代名詞的用法，而 kind 和 evil 則代表某種性格，與前一組並不相似。

Cosine Similarity 在 NLP 很多任務中都用的到，像是通過相似度來做文本分類，或是在之前聊過的資訊檢索中，比較 user query 和每一個文檔之間的相似性。

這裡補充一下 IR 的內容，相較於 TF-IDF 或 BM25 的稀疏檢索 ( Sparse Retrieval )，利用詞向量判斷相似性的做法我們叫做密集檢索 ( Dense Retrieval )，雖然可以有更好表現，但也因為計算量很大而效率較低。

明天要開始挑戰 Transformer 的架構啦！這個部分和前面比起來就複雜多了，所以我會分兩篇來介紹。

推薦文章

• cosine-similarity
• The Role of Cosine Similarity in Vector Space and its Relevance in SEO
• Gensim 官方文件學習筆記